[6.x] 统计量与抽样分布¶

基本概念¶

• 总体与个体：一个统计问题总有它明确的研究对象，研究对象的全体称为总体（母体），总体中的每个成员称为个体；
• 总体容量：总体中包含的个体数；
  • 有限总体是容量有限的总体；
  • 无限总体是容量无限的总体，通常将容量非常大的总体也按无限总体处理；
• 随机样本：为推测总体的分布及其各种特征，按一定规则从总体中抽取若干个体进行观察试验，以获得关于总体的信息，这一过程称为抽样，所抽取的部分个体称为样本，通常记为 \(X=(X_1,X_2,...,X_n)\)；
• 样本容量：样本中所包含的个体数目 \(n\)；
  • 注意，每一个样本 \(X_i\) 都是随机变量，维数与总体一致；
• 简单随机样本：满足代表性和独立性的样本称为简单随机样本(Simple Random Sample)，获得简单随机样本的抽样方法称为简单随机抽样；
  • 代表性：\(X_1,X_2,...,X_n\) 中的每一个与所考察的总体 \(X\) 都有相同的分布；
  • 独立性：\(X_1,X_2,...,X_n\) 是相互独立的随机变量；

后面提到的所有样本，指的都是简单随机样本。

• 若总体有分布函数 \(F(x)\)，则样本具有联合分布函数 \(F_n(x_1,x_2,...,x_n)=\prod_{i=1}^{n}F(x_i)\)；
• 若总体为连续型（或离散型）随机变量，其概率密度函数（或分布律）为 \(f(x)\)，则样本具有联合密度函数（或联合分布律） \(f_n(x_1,x_2,...,x_n)=\prod_{i=1}^{n}f(x_i)\)

统计量¶

设 \((X_1,X_2,...,X_n)\) 是来自总体 \(X\) 的一个样本，\(g(X_1,X_2,...,X_n)\) 是 \(X_1,X_2,...,X_n\) 的函数，若 \(g\) 中不含任何未知参数，则称 \(g(X_1,X_2,...,X_n)\) 为一统计量。换言之，统计量是样本的不含任何未知参数的函数。

• 统计量仍然为随机变量；
• 统计量的分布（称为抽样分布）一般与总体分布有关，可以依赖未知参数；
• 当样本的观察值确定时，统计量的值也就随之确定了；

样本均值¶

样本均值反映了总体的期望（均值）。

样本均值的性质：

• \(E(\overline{X})=\mu\)，\(Var(\overline{X})=\sigma^2/n\)
• \(\sum_{i=1}^{n}(X_i-\overline{X})=0\)；
• 数据观测值与样本均值的偏差平方和最小，即在形如 \(\sum(X_i-c)^2\) 的函数中，\(\sum(X_i-\overline{X})^2\)最小；
• 若总体服从 \(N(\mu,\sigma^2)\)，则 \(\overline{X}\) 的精确分布为 \(N(\mu,\sigma^2/n)\)；
• 若总体分布未知或不是正态分布，则当 \(n\) 较大时，\(\overline{X}\) 近似服从 \(N(\mu,\sigma^2/n)\)；

样本方差¶

样本方差反映了总体的方差，常作为总体方差 \(\sigma^2\) 的无偏估计。

样本方差的性质：

• \(E(S^2)=\sigma^2\)；
• \(\sum(X_i-\overline{X})^2=\sum X_i^2-\frac{1}{n}(\sum X_i)^2=\sum X_i^2-n\overline{X}^2\)；

此外，\(S=\sqrt{S^2}=\sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\overline{X})^2}\) 称为样本标准差。

样本 k 阶矩¶

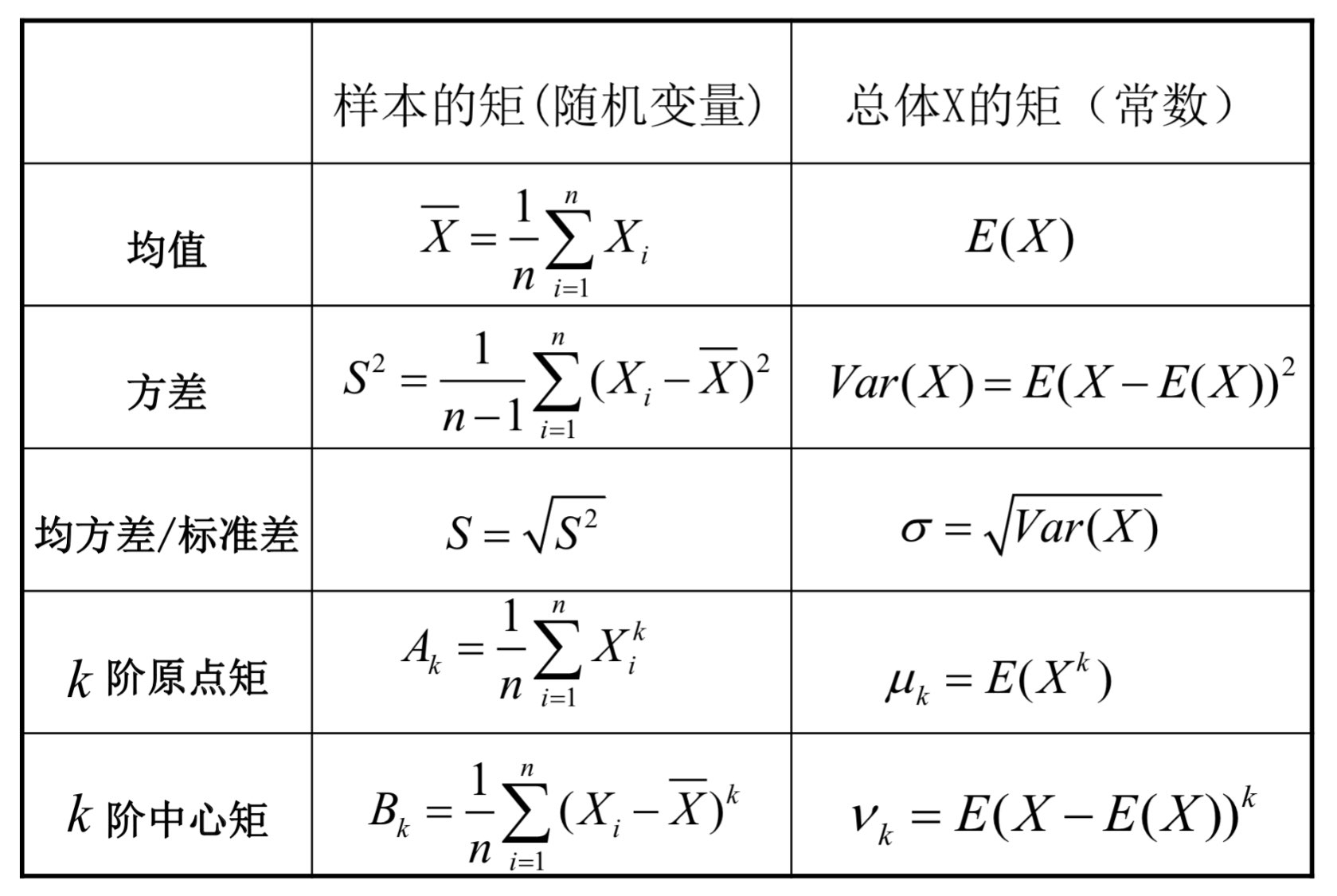
样本 \(k\) 阶（原点）矩，常作为总体 \(j=k\) 阶原点矩 \(\mu_k\) 的估计：

样本 \(k\) 阶中心距，常作为总体 \(j=k\) 阶中心矩 \(\nu_k\) 的估计，\(B_2\) 可作为总体方差 \(\sigma^2\) 的有偏估计：

样本 \(k\) 阶矩的性质：

• 假设 \(X_1,X_2,...,X_n\) 是 \(X\) 中抽取的样本，\(\mu_k=E(X^k)\) 存在，由辛钦大数定律可知：
  \(A_k=\frac{1}{n}\sum_{i=1}^{n}X_i^k\xrightarrow{P}\mu_k,\;\;k=1,2,...\)

样本与总体的各阶矩对比表：

三大抽样分布¶

统计量的分布称为抽样分布(Sampling Distribution)。

χ² 分布 / 卡方分布¶

设 \(X_1,X_2,...,X_n\) 为独立同分布，服从 \(N(0,1)\)。则称 \(\chi_{n}^{2}=\sum_{i=1}^{n}X_i^2\) 服从自由度为 \(n\) 的 \(\chi^2\) 分布，记 \(\chi_{n}^{2}\sim \chi^2(n)\)。

\(\chi^2\) 分布的密度函数（不要求）：

\(\chi^2\) 分布有如下性质：

• 设 \(X \sim \chi^2(n)\)，则有 \(E(X)=n\)，\(Var(X)=2n\)；
• 设 \(Y_1 \sim \chi^2(m)\)，\(Y_2\sim\chi^2(n)\)，且两者互相独立，则 \(Y_1+Y_2\sim \chi^2(m+n)\)；
  • 这一性质被称为 \(\chi^2\) 分布的可加性，可以推广到有限个相加的情形；
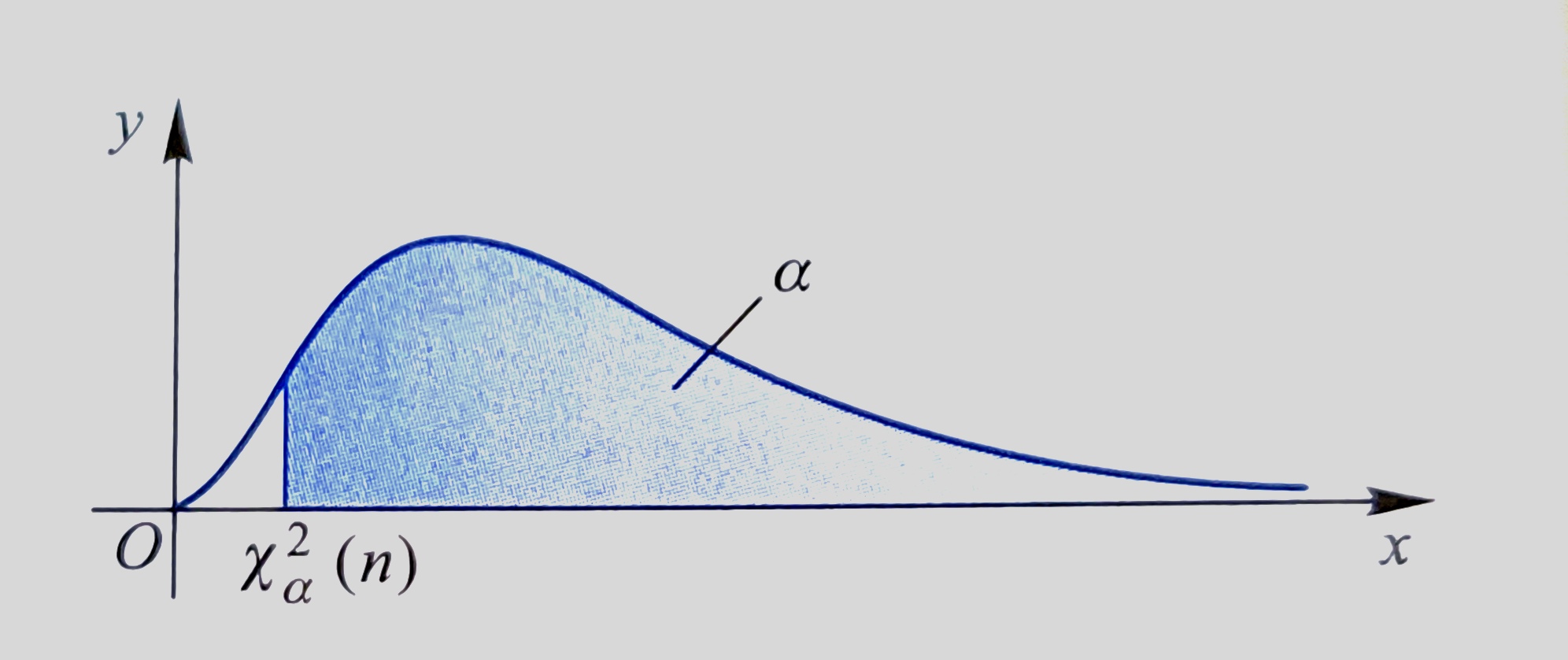
• \(\chi^2\) 分布的上 \(\alpha\) 分位数：
  对于给定的正数 \(\alpha,\;0<\alpha<1\)，称满足条件 \(P\{\chi^2>\chi^2_\alpha(n)\}=\int^{+\infty}_{\chi^2_\alpha(n)}f_{\chi^2}(x)\mathrm{d}x=\alpha\) 的点 \(\chi^2_{\alpha}(n)\) 为 \(\chi^2(n)\) 分布的上 \(\alpha\) 分位数；

t 分布 / 学生氏分布¶

设 \(X\sim N(0,1)\)，\(Y\sim \chi^2(n)\)，且 \(X,Y\) 相互独立，则称随机变量 \(T=\frac{X}{\sqrt{Y/n}}\) 服从自由度为 \(n\) 的 \(t\) 分布，记做 \(T\sim t(n)\)。

\(t\) 分布的密度函数（不要求）：

其中 \(\Gamma(\alpha)=\int_0^{+\infty}t^{\alpha-1}e^{-t}\mathrm{d}t\)，\(\Gamma(\alpha+1)=\alpha\Gamma(\alpha)=\alpha!(if\;\alpha\in\Z)\)，\(\Gamma(0.5)=\sqrt{\pi}\)。

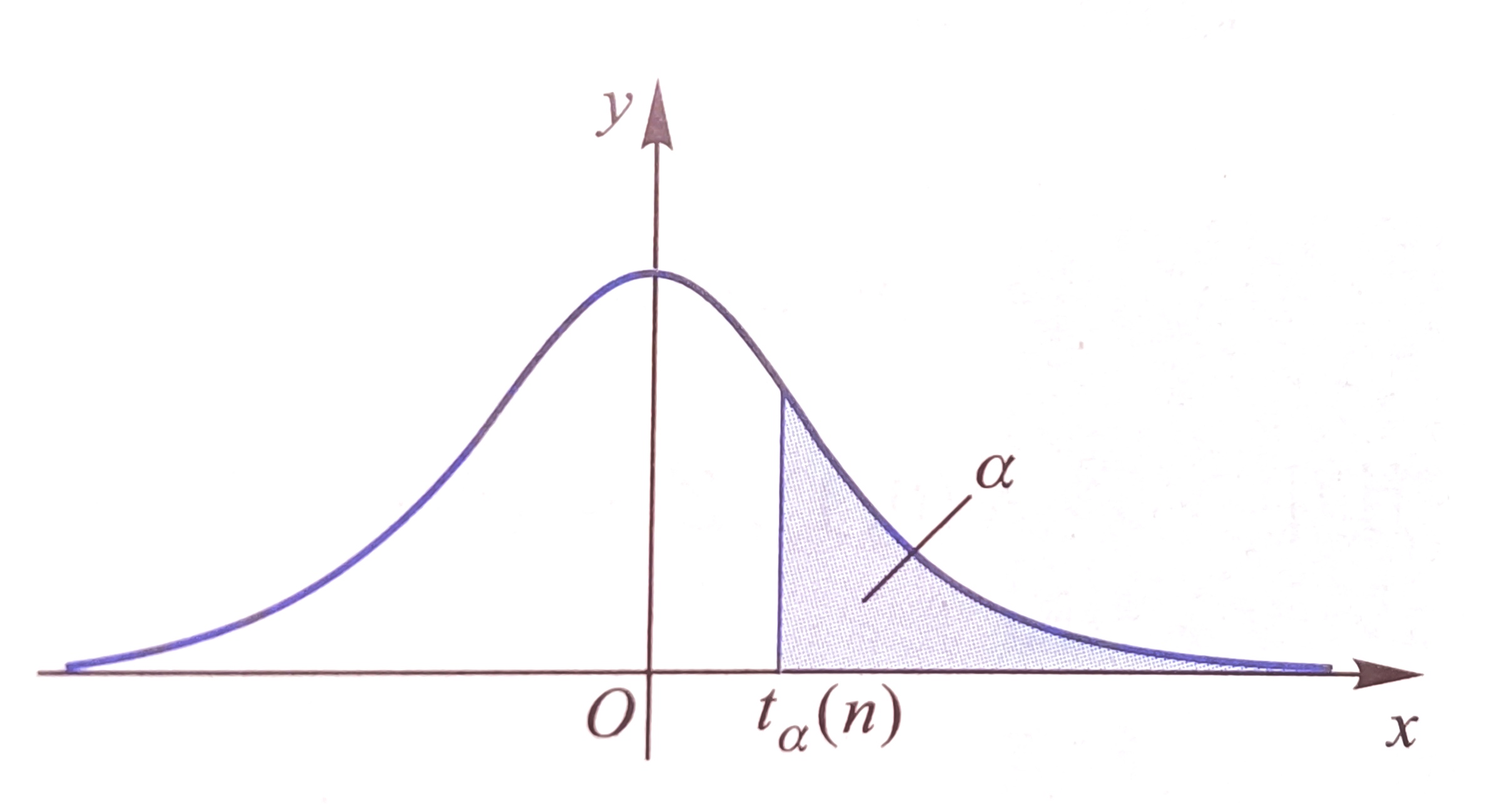
\(t\) 分布有如下性质：

• 设 \(T\sim t(n)\)，则当 \(n\geq 2\) 时，有 \(E(T)=0\)；当 \(n\geq 3\) 时，有 \(Var(T)=\frac{n}{n-2}\)；
• 当 \(n\) 足够大时，\(t\) 分布近似于标准正态分布 \(N(0,1)\)；
• 设 \(T\sim t(n)\)，\(N\sim N(0,1)\)，则对任意的 \(n\geq 1\)，都存在 \(a_0>0\)，使得 \(P(|T|\geq a_0)\geq P(|N|\geq a_0)\)；
• \(t_{1-\alpha}(n)=-t_{\alpha}(n)\)；

F 分布¶

设 \(U\sim\chi^2(n_1)\)，\(V\sim \chi^2(n_2)\)，且 \(U,V\) 相互独立，则称随机变量 \(F=\frac{U/n_1}{V/n_2}\) 服从自由度为 \((n_1,n_2)\) 的 \(F\) 分布，记 \(F\sim F(n_1,n_2)\)。

\(F\) 分布的密度函数（不要求）：

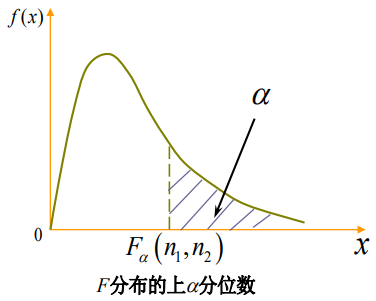
\(F\) 分布有如下性质：

• 设 \(F\sim F(n_1,n_2)\)，则 \(F^{-1}\sim F(n_2,n_1)\)；
• 设 \(X\sim t(n)\)，则 \(X^2\sim F(1,n)\)；
• \(F_{1-\alpha}(n_1,n_2)=\frac{1}{F_{\alpha}(n_2,n_1)}\)；

正态总体下的抽样分布¶

设 \(X_1,X_2,...,X_n\) 是来自正态总体 \(N(\mu,\sigma^2)\) 的样本，\(\overline{X}\) 是样本均值，\(S^2\) 是样本方差，则有：

1. \(\overline{X}\sim N(\mu,\frac{\sigma^2}{n})\)；
2. \(\frac{(n-1)S^2}{\sigma^2}\sim \chi^2(n-1)\)；
3. \(\overline{X}\) 与 \(S^2\) 相互独立；
4. \(\frac{\overline{X} - \mu}{S/\sqrt{n}}\sim t(n-1)\)；
5. 这里注意区别一下：\(\frac{\overline{X} - \mu}{\sigma/\sqrt{n}}\sim N(0,1)\)；

设 \(X_1,X_2,...,X_{n_1}\) 和 \(Y_1,Y_2,...,Y_{n_2}\) 是分别来自正态总体 \(N(\mu_1,\sigma_1^2)\) 和 \(N(\mu_2,\sigma_2^2)\)，并且它们相互独立，\(\overline{X},\overline{Y}\) 是样本均值，\(S_1^2,S_2^2\) 是样本方差，则有：

1. \(\frac{S_1^2/\sigma_1^2}{S_2^2/\sigma^2_2}\sim F(n_1-1,n_2-1)\)；
2. \(\frac{(\overline{X}-\overline{Y})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_1}+\frac{\sigma_{2}^{2}}{n_2}}} \sim N(0,1)\)；
3. 当 \(\sigma_1^2=\sigma_2^2=\sigma^2\) 时：
   \(\frac{(\overline X - \overline Y) - (\mu_1-\mu_2)}{S_\omega\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\sim t(n_1+n_2-2)\)，其中 \(S^2_\omega=\frac{(n_1-1)S_1^2+(n_2-1)S^2_2}{n_1+n_2-2}\)；

激励

评论